The Segment Addition Postulate

The phrase "Segment Addition Postulate" can be a little intimidating, especially at the beginning of a Geometry or Honors Geometry course.

However, we will show you that this postulate is nothing more than breaking sticks...and then putting them back together. You can do that right? Okay, good. So let's simplify this "intimidating" topic.

Activity

In order to get an accurate visual, you need to gather some materials. First, go find a stick in your back yard - or use a skewer like the one shown here (but be careful of the sharp end.) Licorice is a safe alternative, although you will have to resist eating it (at least until after the activity.)

Next, measure the length of your object. Our skewer is 8 inches long.

  
Break the object into 2 pieces and measure the length of both pieces. Our pieces are 2 inches, and 6 inches long.

Finally, put the two pieces back together. Measure the length of the skewer or stick now that it is put back together.

Our skewer is still 8 inches like it was originally. Does this seem easy and obvious? Good, it should!

Congratulations, you just modeled the postulate.


Formal Definition


Now, to get a little more technical. The math definition of a postulate says that if point Q is between points P and R on a line, then PQ + QR = PR. Take a look at the diagram below.

 

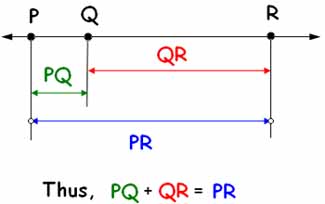
All this means is...if you take one piece of a segment (PQ), and add it to another piece of a segment (QR), you get the entire segment (PR). "The sum of the parts equals the whole."

Return from Segment Addition Postulate to Free Geometry Help.

 

 

 

 
Untitled Document

Stay connected

     
.


Home │ Site Search │ Math Help Blog │ Help Keep GradeA Free


Written by Team GradeAmathhelp.com, all rights reserved.