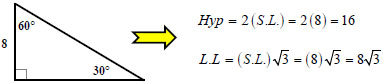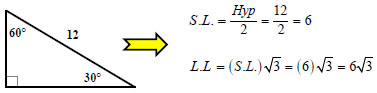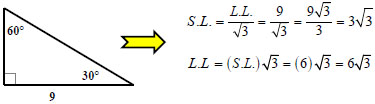The 30-60-90 Triangle

A 30-60-90 triangle is a special right triangle. The other type of special right triangle is 45-45-90. These numbers represent the degree measures of the angles.

The General Formula of a 30-60-90 Triangle

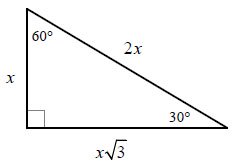
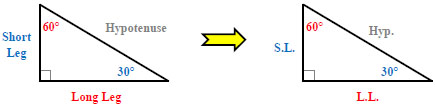
Before we explain how to find the missing sides, we need to give specific names to each of the sides. For example, the side across from the right angle is always called the hypotenuse (you probably already knew that from the pythagorean theorem). See below.

The side across from the 60° angle is known as the long leg (L.L.).

The side across from the 90° angle is known as the hypotenuse (Hyp.).

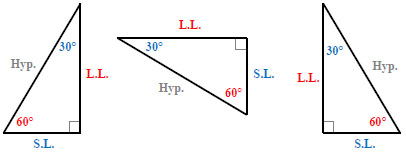
Important: Regardless of what direction the triangle is turned, the sides are still named according to their relationship to the angles.

Look at the examples below: The sides are always across from their angle

You will always be given one of the three sides. What you do from there depends on which side that you are given. Consider each case below.

ownload GradeA's 30-60-90 triangle study guide (.pdf)!

Case #1: I know the Short Leg

Case #2: I know the Hypotenuse

Case #3: I know the Long Leg

Learn about the other special right tirangle: 45-45-90 triangle.

You may also be interest in other geometry formulas, or geometry help.

Or visit the GradeA homepage for more free math help.