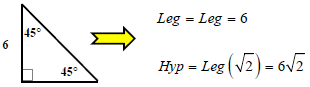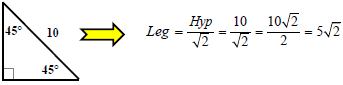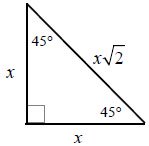
45-45-90 Triangle

A 45-45-90 triangle is a special right triangle. The other type of special right triangle is 30-60-90. These numbers represent the degree measures of the angles.

The example below shows the basic ratios of the triangle. Regardless of what the "x" value is, the ratios will always hold true.
The General Formula of a 45-45-90 Triangle

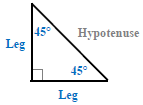
Because both of the base angles are equal to 45°, the converse of the isosceles triangle theorem tells us that both of the legs are equal.

Therefore, we will refer to the two congruent sides as legs, and the other side (which is opposite the right angle) as the hypotenuse.

More information about the hypotenuse from the pythagorean theorem.

You will always be given one of the three sides. What you do from there depends on which side that you are given. Consider both cases below.

Case #1: I know a Leg

Case #2: I know the Hypotenuse

Please notice that in both cases you are either multipying by the square root of 2 or you are dividing by the square root of 2. When you divide by a square root, don't forget to rationalize the denominator by multiplying both the top and the bottom of the fraction by the radical. Good luck!

Learn about the other special right triangle the 30-60-90 or you may also be interested in other geometry formulas.

Return from 45-45-90 triangle to free geometry help.

Visit the GradeA homepage for more free math help.