Algebra Absolute Value

Curious what this algebra absolute value stuff is all about?

The formal definition of the absolute value of a number goes as follows:

The absolute value of a number is the distance that number is from zero on a number line.

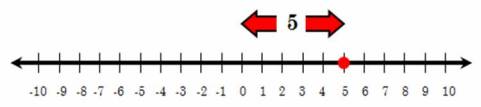
Take a look at the pictorial representation below. If you need it, get more information about the number line.

To find|5| (known as "the absolute value of 5") find the distance that 5 is from 0.

Because 5 is 5 units from 0, that means that|5| = 5.

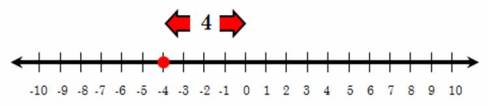
Let's look at another example. Now lets find |-4| .

Because -4 is 4 unit from 0, that means that |-4| = 4.

Using the two examples above, can you find the pattern for evaluating algebra absolute values? Positive Numbers: Notice that for every positive number, the distance the number is from 0 is the same as the number.

|Positive Number| = Positive Number

Negative Numbers: Notice now that the number is the same, but the negative sign is dropped. You know that a distance cannot be negative (you can't be negative 6 feet tall!). Because absolute value is the distance from zero, it also cannot be negative!

|Negative Number| = Number without the Negative Sign

There's a lot more to an algebra absolute value than just the definition.

Return to more free algebra help.