Eulers Formula

Eulers formula compares the number of faces, edges, and vertices of a polyhedron.

The famous mathematician Leonard Euler is credited with the discovery of the formula, hence the name.

The formula is shown below:

V + F = E + 2

V = number of vertices

F = number of faces

E = number of edges

  

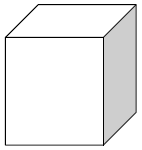
This formula applies to polyhedron, which are three-dimensional figures comprised of polygons. Take a look at a very basic example below. The figure shown is a cube, which has 6 sides that are all squares.

V = 8

F = 6

E = 12

V + F = E + 2

8 + 6 = 12 + 2

14 = 14


   

As it was state previously, this formula applies to all convex polyhedron. The cube is just one example.


A Tip to Help You Remember the Formula

 

Again, the formula is V + F = E + 2. But, If you look at the formula backwards, in other words 2 + E = F + V, now the numbers and letters are in alphabetical order. This little trick will help you to easily remember the formula, so use it to help yourself!

Remember, because it is an equation, the sides can be flipped. If you use this trick, you will have no problem remembering this useful geometric formula.


More Information

Read more about Leonard Euler's contributions to mathematics. Most notably, you can thank (or criticize!) him for the development of function notation.

 

Return from Eulers Formula to more Free Geometry Help or visit the GradeA homepage for more free math help.

 

 
Untitled Document

Stay connected

     
.


Home │ Site Search │ Math Help Blog │ Help Keep GradeA Free


Written by Team GradeAmathhelp.com, all rights reserved.