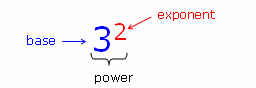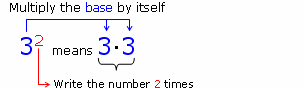Exponents and Powers

Don't be afraid when you see something like 3².  Numbers like the 2 shown are called exponents, and they have a special meaning in math.  The number 3 is called the base, and the entire expression, 3² is a power.

A power is a multiplication problem.  Mathematicians are lazy, so sometimes they make shortcuts for writing problems faster. 

Whatever the base is (bigger number) that is the number that is going to get multiplied.  The exponent (smaller number) is the number of times you will multiply the base times itself. 

Picture explanation: 

 Sometimes, powers are evaluated like so:  3³ = 3·3·3 = 9·3 = 27

They can also apply to variables: 

x³ = x·x·x      or     x⁵ = x·x·x·x·x     or     y⁴ = y·y·y·y

Listen carefully:  Any power where the "raised number" is 0 is equal to 1.

I know this sounds strange, but believe us it is true.  It always equals 1!

Examples:  3⁰ = 1   ◊   9⁰ = 1   ◊   x⁰ = 1   ◊   (any number)⁰ = 1

So, now that you know about exponents, why not learn about subscripts?  Take a look at our page on calculating slope to learn why 3² isn't 3₂!

Other pre-algebra topics or the GradeA homepage.