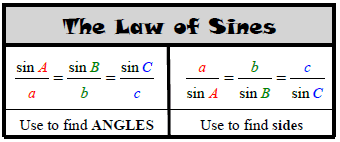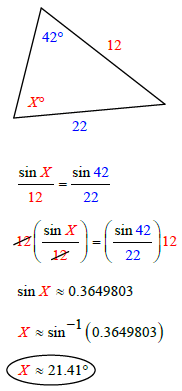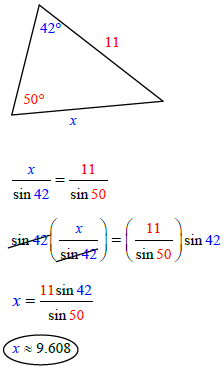The Law of Sines (Sine Rule)

The law of sines is used to finding missing sides and angles of triangles.

Before you attempt to use the formula shown above, please be sure that you understand the basics of trigonometry first. You must also have strong algebra skills, particularly with solving proportions. Before going any further, please be certain you are able to:

• Evaluate the sine of angle using the sin function
• Find the measure of an angle using the inverse sine function: sin^-1
• Solve a proportion involving trig functions.
• Understand the naming conventions for triangles (see below)

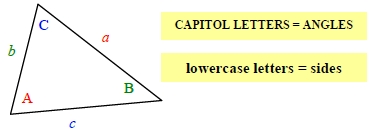
First, you must understand what the letters a, b, c and A, B, C represent in the formula. The corresponding letters (a & A, b & B, c & C) represent the side and the angle across from it. Please see the figure below.

Note: the letters used are arbitrary. As long as you match the side with the angle across from it, the formula will work!

The formula is listed in two forms: the standard form (used for sides) and the reciprocal form (used for angles). See below.

Q: Why are there 3 parts to the equation?

A: The formula states that all 3 ratios are equal. You will never use all 3 of them at the same time. Instead, you will pick 2 of the 3, depending on what information you are given. The formula could be written as...

Q: Why are there two different forms of the law of sines?

A: The formula used for angles is known as the reciprocal form. In fact, it is not needed. We simply use it to make the algebra easier when we are solving problems to find a missing angle.

Q: What is the "Ambiguous Case?"

A: Please read below.

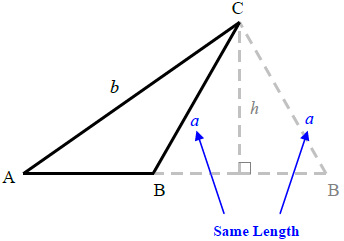
A special case of the law of sines arises when the triangle is in the form Side-Side-Angle (SSA). This is easy to remember because SSA is a curse word, and you will be cursing at your paper whenever you have to deal with it.

When you are given angle A, side a, and side b, it is possible that two different triangles can be made to fit the conditions.

• Two triangles are formed when h < a < b, where h = bsinA.

Notice in the figure above that side a can "swing" to form either an obtuse triangle or an acute triangle, but angle angle A and side b are not change.

The figure at the right demonstrate the two possible cases. Case 1 is the entire triangle. Case 2 is the grey shaded triangle.

Example to find an Angle		Example to find a Side