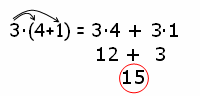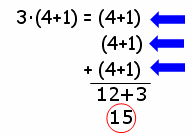Common Math Properties

The following math properties are formally introduced in algebra classes, but they are taught in many elementary schools. You probably don't even realize that you already know many of these properties. For example, the commutative property basically states you can add in any order: 6 + 5 is the same as 5 + 6.

Vist our pages dedicated to the math property of equality or math clue words.

You should also be sure to understand the order of operations before attempting to understand these math properties.

Each property is listed below. On the left side of the table we show the general form – using all letters.  We know properties can be confusing when too many variables are use, so we also give an example with numbers on the right side of the table as well.  Aim to learn the general form, but use the numeric form as your "training wheels."

The associative property indicates that the grouping of numbers does not matter. By "grouping" we simply mean where the parentheses are placed. Take a look:

Notice how the order of the numbers did not change.  In the examples with numbers, the order always goes 3, 5, 1. 

How can we remember the name of this math property?  One possibility is to think of the word associate – which is another word for friends.  You probably have different groups of friends and you hang out with them at different times.  The associative property deals with changing groups (parentheses).  You don’t change the order, you just change the groups. 

The commutative property (like we described at the top of the math properties page) deals with the order that add or multiply numbers.

The distributive property will be most useful when one of the numbers inside the parentheses is a variable.  Certain math properties are only useful in some situations.

he word identity means “who you are.”  You may have heard of identity theft.  In math, we want a number to keep its same identity – in other words, stay as the same number.  What number would you have to add to a number to keep it the same?  What about multiplication?

he identity operator of addition is 0 because any number plus 0 is always equal to that number – and yes, you can switch the order!

The identity operator of multiplication is 1 because any number times 1 is always equal to that number – again you can use the commutative prop!

This math property states that any number multiplied by zero will always be equal to zero.  You probably already knew this one.

Return to other pre algebra math problems or visit the GradeA homepage.