All About Polynomials

A main topic in algebra classes is polynomials. There are many subtopics of this topic, including adding, subtracting, multiplying, and dividing.

Terms are seperated by + and - signs. Poly's with 1, 2, or 3 terms have specific names, while poly's of 4 or more terms are simply called polynomials of # terms. Take a look at the table below.

Again, all you are looking for is the number of terms. When there are 1, 2, or 3 the poly is given the special names monomial, binomial, trinomial, respectively. If there are more than 3, then it is simply called a poly of that many terms.

The degree of a poly is determined by the exponents. In fact, it is determined by the largest exponent. Take a look at this table...

Notice that we are no longer interested in the number of terms, but simply the degree of the exponent.

Often polynomials will be referred to by both the number of terms and the degree. Take a look at the two examples below.

For simplicity, it is often preferred to put a poly into standard form. This means that the terms are place in descending order (highest to lowest) according to their degree.

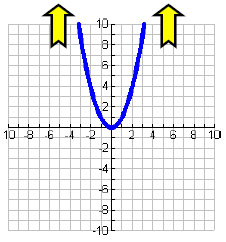
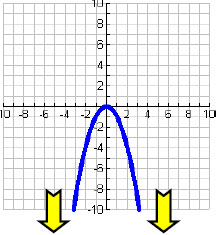
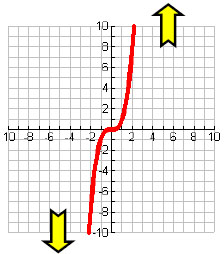
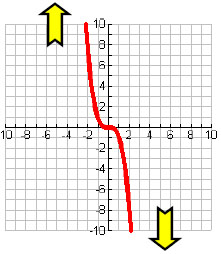
The end behavior of a graph is what happens at the far left and the far right. Two factors determine the end behavior: positive or negative, and whether the degree is even or odd.

For the examples below, we will use x² and x³, but the end behavior will be the same for any even degree or any odd degree. However, keep in mind that what happens "in the middle" will change...

Even Degree (ex: x2, x4, x6,...)
Positive: Up, Up	Negative: Down, Down

Odd Degree (ex: x, x3, x5,...)
Positive: Down, Up	Negative: Up, Down

Knowing the general shape and end behavior is an important step towards understanding polys. With a little practice, you will know how to perform all of the operations associated with polynomials. Take a look at how to perform polynomials division.

Return to free algebra help for more help or visit the GradeA homepage.

Stay connected