Combining Like Terms

Before you start combining like terms, you first need to know what the meaning of a like term really is. First, you need to know that a term is a number, or a number and a variable multiplied together. Terms are separated by addition and subtraction signs (+ and -).

Examples of terms: (assuming our variable is x)

x, 3x, 9, 6x2, -2x, 14, 8x3, -6, 2x2, 7x, -x2, 31

Each term above is either a number, or a number times a letter. The letter may also have an exponent.

Definition of Like Terms:

Terms that have the same variable raised to the same power.

Like Terms (#'s) Like Terms (x) Like Terms (x2) Unlike Terms
9 and 7 4x and -2x 3x2 and x2 4 and 3x

More examples of unlike terms are below...

  • 5x and 3x2 are unlike because the exponents are different.
  • 4x and 3y are unlike because the variables are different.
  

 

Color-Coding the Different Groups of Terms

Beginning level algebra will only deal with 3 different groups in 1 variable:

  • The numbers (black): 1, 9, 0, -6, 14, -8, ...

  • The x's (red): x, 4x, -2x, 6x, -12x, ...

  • The x2's (blue): x2, 4x2, -3x2, 9x2, ...

 

By following these color patterns, it will make combining like terms much easier at the start. You can add different variables and higher powers once you get more familiar with the concept

Combining Like Terms of an Expression

Expression: A set of terms separated by + and - signs.

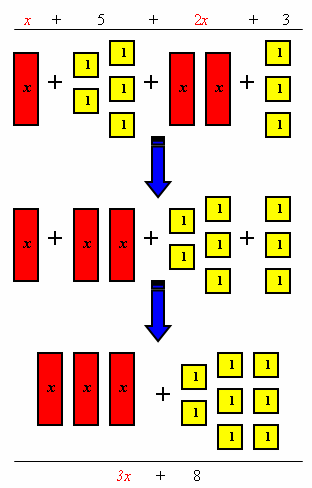
Look at the expression at the right: x + 5 + 2x + 3

Reorder (commutative property): x + 2x + 5 + 3

Combine the different groups: 3x + 8

Pictorial Explanation:

combining like terms  

More Examples of Combining Like Terms

Example #1 Example #2 Example #3
3x + 5 + x 5 + 4x + 2x + 2 5x2 + 3x + 4x
4x + 5 6x + 7 5x2 + 7x

A further look at combing like terms, determining the difference between an equation and expression, and other key algebra concepts are here.

Combining like terms is easy, let's look at other algebra topics.

For all your free math help needs, the GradeA homepage.

 

 

 
Untitled Document

Stay connected

     
.


Home │ Site Search │ Math Help Blog │ Help Keep GradeA Free


Written by Team GradeAmathhelp.com, all rights reserved.