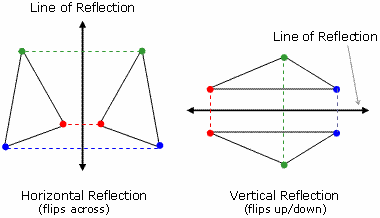
Basic Transformation Geometry

For transformation geometry there are two basic types:  rigid transformations and non-rigid transformations.  This page will deal with three rigid transformations known as translations, reflections and rotations.

In short, a transformation is a copy of a geometric figure, where the copy holds some certain properties.  Think of when you copy/paste a picture on your computer.

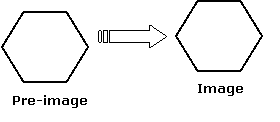
The original figure is called the pre-image; the new (copied) picture is called the image of the transformation. 

A rigid transformation is one in which the pre-image and the image both has the exact same size and shape.

 

Translations - Each Point is Moved the Same Way

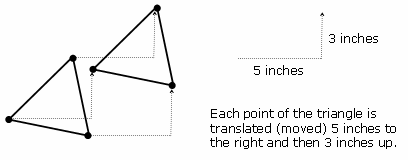
The most basic transformation is the translation.  The formal definition of a translation is "every point of the pre-image is moved the same distance in the same direction to form the image."  Take a look at the picture below for some clarification.

Each translation follows a rule.  In this case, the rule is "5 to the right and 3 up."  You can also translate a pre-image to the left, down, or any combination of two of the four directions.

More advanced transformation geometry is done on the coordinate plane.  The transformation for this example would be T(x, y) = (x+5, y+3).

 

Reflections - Like Looking in a Mirror

A reflection is a "flip" of an object over a line.  Let's look at two very common reflections:  a horizontal reflection and a vertical reflection.

Notice the colored vertices for each of the triangles.  The line of reflection is equidistant from both red points, blue points, and green points.  In other words, the line of reflection is directly in the middle of both points. 

Examples of transformation geometry in the coordinate plane...

• Reflection over x-axis:      T(x, y) = (x, -y)

• Reflection over y-axis:      T(x, y) = (-x, y)

• Reflection over line y = x:  T(x, y) = (y, x)

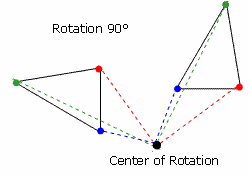
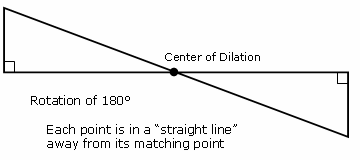
A rotation is a transformation that is performed by "spinning" the object around a fixed point known as the center of rotation.  You can rotate your object at any degree measure, but 90° and 180° are two of the most common.  Also, rotations are done counterclockwise!

The figure shown at the right is a rotation of 90° rotated around the center of rotation.  Notice that all of the colored lines are the same distance from the center or rotation than than are from the point.  Also all the colored lines form 90° angles.  That's what makes the rotation a rotation of 90°.

More transformation geometry in the coordinate plane...

• Rotation 180° around the origin:  T(x, y) = (-x, -y)

Looking for more examples of transformation geometry?  Please browse our free worksheets database.

Return to other free geometry help topics.

Return to the GradeA homepage.