Trigonometric Identities

Trigonometric identities are properties of trig functions that always hold true. Knowing these identities can make solving trigonometric problems much easier because you can simply the equation very easily.

As a simpler example of what an identify is, look at the identity property of addition: x + 0 = x.

Notice how this equation holds true for any value of x. Essentially, it says add 0 to any number and you will still have that number.

Of course, trig identities are more complex than simple addition, but the idea remains the same. No matter what the value is, the equation will always hold true.

  

For trigonometry, the values are angles (either in degree or radian measure).

   

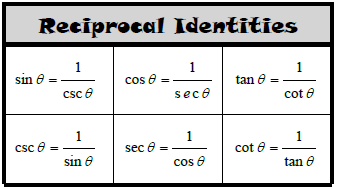
The Pythagorean Identities are probably the most "famous" of the trigidentities. Particularly the starred equation above: "sine squared plus cosines squared equals 1" is used often in trig and calculus classes.

Other identities are also listed below. The reciprocal identites are often taught early in a trigonometry curriculum.

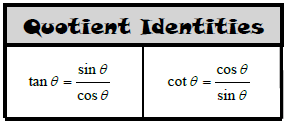
By memorizing the reciprocal and quotient identities that are shown at the right, you can use the unit circle to evaluate all six trigonometric functions instead of just the sin and the cos.

Note: The "circle with the line through it" is the Greek letter "Theta" and is simply a variable that is often used in trigonometry to represent an angle.

 

We know some of these identities might seem a little challenging, and you might be wondering what they are used for... The simple answer is they are used to simplify equations. If you look at the quotient identities above, you can see that sin divided by cos is equal to the tan. Isn't it a lot simplier to just write tan? That's the whole idea - make life easier on yourself. Good luck!

Additional Information

Return from Trigonometric Identities to the main Trigonometry page.

Check out GradeA's law of sines page to see how to solve for missing sides of oblique triangles.

 

You can also visit the GradeA homepage for more free math help.
Untitled Document

Stay connected

     
.


Home │ Site Search │ Math Help Blog │ Help Keep GradeA Free


Written by Team GradeAmathhelp.com, all rights reserved.