A Factor Tree Makes Factoring Easy

An easy was to factor a number is by making a factor tree.  To make a tree, simply write the number you want to factor at the top of your paper.

From there, make branches of factors - numbers that multiply to give you the original number.  Next, take each of those numbers and break those down into more factors.  Continue until all the remaining numbers are prime numbers and cannot be factored anymore.

Have trouble understanding that explanation?  We have two examples below:

Factor trees of 36 and 48.

   

Example 1: Factor 36

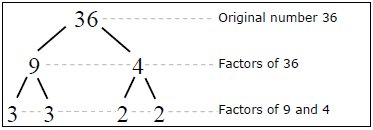
Here is an example of how to factor the number 36:

Factor tree of 48

    

Now we can easily see the factors of 36 are 3, 3, 2, and 2. All this means is that if you take those numbers and multiply them together: 3(3)(2)(2) = 36.

We can also write this in a fancier wasy using exponents: 36 = 22•32

Factoring is the the process of breaking a part a multiplication problem.

Please note:  You did not have to choose 9 and 4 as the first two "branches" of the tree.  You can pick any two numbers that multiply to make 36.  Other possibilities are 6 & 6, 3 & 12, and 2 & 18.

 

Example 2: Factor 48

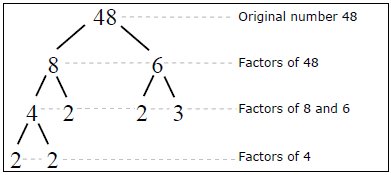
Here is an example of how to factor the number 48:

Factor tree of 48

So this means the factors of 48 are 2, 2, 2, 2, and 3. Please notice that you only count the numbers on the last branches. And don't forget to count them all. It is easy to lose the extra 2 that is branched off of the 8.

  

In exponent form you have: 48 = 24•3

 

For more great factoring tips, return from factor tree to how to factor.

 

 
Untitled Document

Stay connected

     
.


Home │ Site Search │ Math Help Blog │ Help Keep GradeA Free


Written by Team GradeAmathhelp.com, all rights reserved.