A List of Perfect Squares

Perfect squares are numbers that are created when you take a whole number times itself. They are used in many different topics in algebra, including factoring and radicals, and also in other disciplines like geometry.

GradeA's List of Squares

12
=
 1
262
=
 676  
22
=
 4
272
=
 729
32
=
 9
282
=
 784
42
=
 16
292
=
 841
52
=
 25
302
=
 900
62
=
 36
312
=
 961
72
=
 49
322
=
 1024
82
=
 64
332
=
 1089
92
=
 81
342
=
 1156
102
=
 100
352
=
 1225
112
=
 121
362
=
 1296
122
=
 144
372
=
 1369
132
=
 169
382
=
 1444
142
=
 196
392
=
 1521
152
=
 225
402
=
 1600
162
=
 256
412
=
 1681
172
=
 289
422
=
 1764
182
=
 324
432
=
 1849
192
=
 361
442
=
 1936
202
=
 400
452
=
 2025
212
=
 441
462
=
 2116
222
=
 484
472
=
 2209
232
=
 529
482
=
 2304
242
=
 576
492
=
 2401
252
=
 625
502
=
 2500

Why Are They Called "Perfect Squares?"

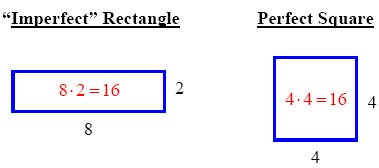
Multiplying a number by itself is given this special name because of the geometrical interpretation. Think of the dimensions of a rectangle. If the numbers are not the same, then you will have an imperfect rectangle. But if the dimensions are the same, meaning the length is the same size as the width, then your rectangle will become a square that is perfect.

Take a look at the figure below to get an idea what we are talking about.

Geometric Interpretation of a Perfect Square

Notice how when the dimensions are the same it creates a square, but when they are different it creates a rectangle. This is why they are called perfect squares!

  

What do you think a perfect cube is? Think about the dimensions of a cube vs. the dimensions of a prism (a box).

I bet you figured it out: A perfect cube is something like 33. A short list of perfect cubes are 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000.

   

View more pre algebra math problems or visit the GradeA homepage.

 
Untitled Document

Stay connected

     
.


Home │ Site Search │ Math Help Blog │ Help Keep GradeA Free


Written by Team GradeAmathhelp.com, all rights reserved.