How to Factor Polynomials

Learning how to factor polynomials does not have to be difficult. GradeA will break down the steps for you, show you simple examples with visual illstrations, and also give you some clever tips and tricks.

Use the following steps to factor your polynomials:

Do you want to know how to solve quadratic equations (ex: x² + 8x + 15 = 0)? Learn how to solve quadratic equations, which is a different type of problem than factoring, so it requires a different process.

If you are taking a basic algebra class, you probably only need to know one type of factoring when you have two terms: its called the difference of two squares. You need to know how to factor the difference of two squares if you want to know how to factor polynomials.

The example shown above is very common factoring problem. It is called the difference of two squares because it is a subtraction problem ("difference" indicates subtraction) and they are perfect squares between there is some number times itself that gives you that number. More about perfect squares.

Here are a few more examples of difference of two squares:

Now, onto the factoring...

Step 1: Find the square root of each term.

Step 2: Factor into two binomials - one plus and one minus.

x² - 16 factors to (x + 4)(x - 4)

4x² - 49 factors to (2x + 7)(2x - 7)

Notice how each factor breaks down as ...

(Term #1 + Term #2)(Term #1 − Term #2)

As you can see, factoring the difference of two squares is pretty easy when you break it down into a few steps. The next section is a little more advanced, but most Algebra 1 classes don't cover the sum and difference of two cubes, so you might be able to skip this section.

Difference of 2 Cubes: (x³− y³) = (x − y)(x² + xy + y²)

Sum of 2 Cubes: (x³ + y³) = (x + y)(x²− xy + y²)

You can factor the sum of 2 cubes, but you cannot factor the sum of 2 squares!

Method 1: Guess & Check. This is best used when the a value is 1 (more info).

Don't forget, after you find the values you are not quite done yet. Because you are using a method involving "guessing" you want to check to be sure you are correct. The easiest way to check a problem like this is to multiply the binomials together with the math FOIL system and see if you get the original problem.

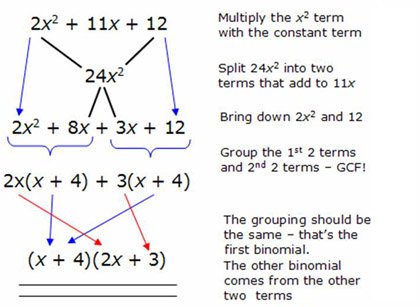
Method 2: The British Method: Best used when the a value is > 1 (more info).

Most beginning students prefer this method when trying to learn how to factor polynomials. The British Method is much more procedural and will always work!

So, of all the ways how to factor polynomials, do you like the British Method?