Greatest Common Factor (GCF)
Finding a greatest common factor (GCF) is the process of identifying the what numbers and variables a group of terms has in common - in other words, what do they share?
In some cases you will "factor it out" and in other cases your teacher will simply ask you to identify it. Finding a GCF is an important skill to learn because it should always be your first step when factoring.
For more information about factoring, try these pages:
Basics of factoring
Factoring in a factor tree. |
|
|
Before looking at some examples, let's break down the phrase:
| Greatest = Largest |
Common = Shared |
Factor = Factored Piece |
Example: 3x2 + 6x
Step 1: Factor each term completely. Help with this
3•x•x + 3•2•x
Step 2: Find all factors that are in common (the same in all terms)
3•x•x + 3•2•x
Step 3: Pull out the GCF and then divide every term by it
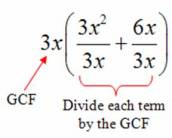
Please remember to put parentheses around the terms, with the GCF on the outside.
Once you get more advanced, you will probably be able to do the division in your head. |
|
|
Step 4: Simplify each term (perform the division)
3x(x + 2)
| More examples of the Greatest Common Factor |
|
|
|
1) 5x3 - 125x
The GCF is 5x. Take that out, and then divide each term
5x(x2 - 25) Now factor the binomial in parentheses farther.
2) 4x3 + 6x + 2x2
The GCF is 2x. Again, take that out.
2x(2x2 + 3 + x)
3) 6x2y + 9xy2
The GCF is 3xy. Notice each term has at least one x and y.
Once you are able to factor the greatest common factor of a polynomial, you will need to learn other factoring techniques. Click here to find out how to factor trinomials and binomials.
Of course, you can learn the basics of how to factor at our factoring main page. We know that factoring can be an intimidating concept for the beginning algebra student, but don't worry, it only takes a little practice.
|
|


