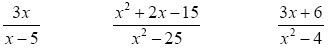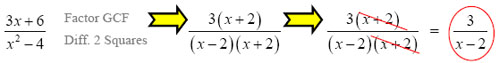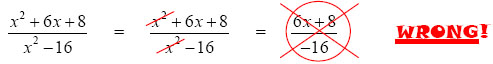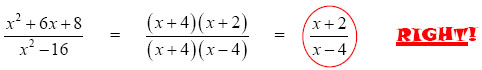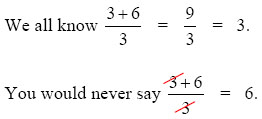Simplify Rational Expressions

In order to simplify rational expressions, you must be strong in factoring.

An algebraic expression, also known as a polynomial, is a series of terms that are added or subracted (more on terms). A rational expression is simply a fraction with an algebraic expression in both the numerator and the denominator.

Examples:

Now that you know what it is, let's move onto simplifying.  

An expression is said to be "simplified" if there are no common factors in the numerator and denominator. In other words, you have to factor the top and bottom and then cancel the common pieces!

Remember: Always factor before you cancel!

Some students will have an urge to cancel terms before they factor. Do not do this! You must always factor first. Take a look at what not to do.

Notice how the student tried to cancel x² before factoring. Incorrect!

Instead, notice how in the follow example, the student first factors, and then cancels the common pieces.

You might be wondering why the first method doesn't work. We know it would be nice if you could do that because it would be a lot easier, but here is why it will not work...

We hope the above example gives you a good idea of why you can't cancel anything you want in an expression.

Now that you know how to simplify rational expressions you can move onto adding, subtracting, multiply, dividing, and even simplifying complex expressions. You may even want to try to solve rational equations.

Return to free algebra help for more algebra resources, or visit the GradeA homepage for other free help topics.